29. Pacific Atlantic Water Flow

Problem Statement

There is an m x n rectangular island that borders both the Pacific Ocean and the Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.

The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).

The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.

Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.

Example 1:

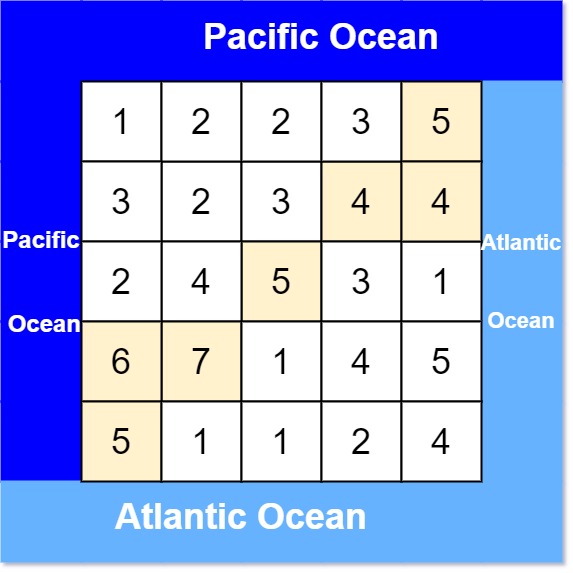
Pacific Atlantic Water Flow Example

Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

Example 2:

Input: heights = [[1]] Output: [[0,0]]

Solution

class Solution:
    def pacificAtlantic(self, heights: list[list[int]]) -> list[list[int]]:
        if not heights:
            return []

        m, n = len(heights), len(heights[0])
        pacific_reachable = set()
        atlantic_reachable = set()

        def dfs(r, c, reachable_set, prev_height):
            # Check boundaries, if already visited, or if water cannot flow up
            if (
                r < 0 or r >= m or c < 0 or c >= n
                or (r, c) in reachable_set
                or heights[r][c] < prev_height
            ):
                return

            reachable_set.add((r, c))
            # Explore neighbors
            dfs(r + 1, c, reachable_set, heights[r][c])
            dfs(r - 1, c, reachable_set, heights[r][c])
            dfs(r, c + 1, reachable_set, heights[r][c])
            dfs(r, c - 1, reachable_set, heights[r][c])

        # Start DFS from all cells bordering the Pacific Ocean
        for r in range(m):
            dfs(r, 0, pacific_reachable, 0)
        for c in range(n):
            dfs(0, c, pacific_reachable, 0)

        # Start DFS from all cells bordering the Atlantic Ocean
        for r in range(m):
            dfs(r, n - 1, atlantic_reachable, 0)
        for c in range(n):
            dfs(m - 1, c, atlantic_reachable, 0)

        # The result is the intersection of the two sets
        return list(pacific_reachable.intersection(atlantic_reachable))

Explanation

Instead of trying to trace the path of water from every cell to the oceans, it's much more efficient to start from the oceans and see which cells the water can reach.

The core idea is to find all cells that can flow to the Pacific and all cells that can flow to the Atlantic. The answer is the intersection of these two sets.

  1. Start from the Oceans: We can think of this as water flowing "uphill" from the oceans. A cell (r, c) can be reached from an ocean if its height is greater than or equal to the height of the cell from which the water is coming.

  2. Two Reachable Sets: We use two sets, pacific_reachable and atlantic_reachable, to store the coordinates of the cells that can be reached by each ocean.

  3. DFS from Borders:

    • We perform a DFS starting from all the cells on the Pacific border (top and left edges). The dfs function explores all reachable cells from a starting point, adding them to the pacific_reachable set.
    • Similarly, we perform another DFS starting from all the cells on the Atlantic border (bottom and right edges), adding reachable cells to the atlantic_reachable set.

  4. DFS Logic: The dfs function takes the current cell (r, c), the appropriate reachable_set, and the prev_height. It only continues the search if the current cell is within bounds, hasn't been visited yet, and its height is greater than or equal to the prev_height (allowing water to flow "uphill").

  5. Intersection: Finally, the cells that can reach both oceans are the ones present in both sets. We find the intersection of pacific_reachable and atlantic_reachable to get our final result.

The time complexity is O(m * n) because we visit each cell at most twice (once for the Pacific DFS and once for the Atlantic DFS). The space complexity is also O(m * n) for the recursion stack and the reachable sets.