50. Linked List Cycle II

Problem Statement

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if (some node in the list is reached again by continuously following the next pointer). Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

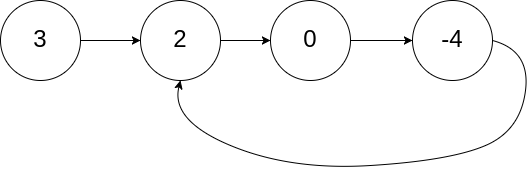
Input: head = [3,2,0,-4], pos = 1 Output: tail connects to node index 1 Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

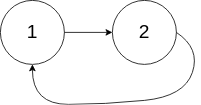
Input: head = [1,2], pos = 0 Output: tail connects to node index 0 Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1 Output: no cycle Explanation: There is no cycle in the linked list.

Solution

# Definition for singly-linked list.
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:
        if not head or not head.next:
            return None

        slow = head
        fast = head

        # Phase 1: Detect if a cycle exists
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                break # Cycle detected
        else:
            # No cycle found
            return None

        # Phase 2: Find the start of the cycle
        # Move one pointer to the head, keep the other at the meeting point.
        # They will meet at the start of the cycle.
        ptr1 = head
        ptr2 = slow # or fast, they are at the same point

        while ptr1 != ptr2:
            ptr1 = ptr1.next
            ptr2 = ptr2.next

        return ptr1

Explanation

This problem is a follow-up to "Linked List Cycle" and also uses Floyd's Cycle-Finding Algorithm (tortoise and hare).

It involves two phases:

Phase 1: Detect if a cycle exists

1. Initialize two pointers, slow and fast, both starting at head.
2. Move slow one step at a time (slow = slow.next).
3. Move fast two steps at a time (fast = fast.next.next).
4. If slow and fast meet at any point, a cycle exists. Break the loop.
5. If fast or fast.next becomes None, it means the end of the list is reached, and there is no cycle. Return None.

Phase 2: Find the start of the cycle

Once a cycle is detected (i.e., slow and fast have met), we can find the starting node of the cycle using a mathematical property:

• Move one pointer (ptr1) back to the head of the list.
• Keep the other pointer (ptr2, which is currently at the meeting point) where it is.
• Move both ptr1 and ptr2 one step at a time.
• The point where they meet again is the start of the cycle.

Why does this work?

Let: - D be the distance from the head to the start of the cycle. - L be the length of the cycle. - M be the distance from the start of the cycle to the meeting point.

When slow and fast meet: - slow has traveled D + M steps. - fast has traveled D + M + nL steps (where n is some integer, meaning fast has completed n full cycles).

Since fast moves twice as fast as slow: 2 * (D + M) = D + M + nL 2D + 2M = D + M + nL D + M = nL D = nL - M D = (n-1)L + (L - M)

This equation D = (n-1)L + (L - M) tells us that the distance from the head to the cycle start (D) is equal to some number of full cycle lengths plus the distance from the meeting point back to the cycle start (L - M).

So, if we move one pointer from the head (ptr1) and another from the meeting point (ptr2), they will both reach the cycle start at the same time.

Time and Space Complexity:

• Time Complexity: O(N), where N is the number of nodes in the linked list. Both phases involve traversing the list at most once.
• Space Complexity: O(1), as we only use a few extra pointers.