49. Linked List Cycle

Problem Statement

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointers. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

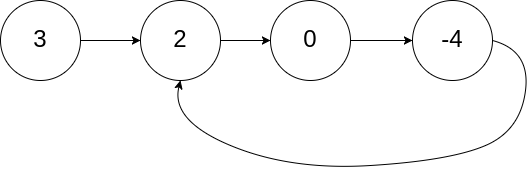
Input: head = [3,2,0,-4], pos = 1 Output: true Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

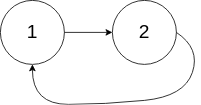
Input: head = [1,2], pos = 0 Output: true Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1 Output: false Explanation: There is no cycle in the linked list.

Solution

# Definition for singly-linked list.
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if not head or not head.next:
            return False

        slow = head
        fast = head.next

        while fast and fast.next:
            if slow == fast:
                return True
            slow = slow.next
            fast = fast.next.next

        return False

Explanation

This problem is a classic application of the Floyd's Cycle-Finding Algorithm, also known as the "tortoise and hare" algorithm.

Core Idea: If there is a cycle in a linked list, a fast pointer will eventually catch up to a slow pointer if they both start at the beginning and the fast pointer moves twice as fast as the slow pointer.

1. Initialize Pointers:

   • slow pointer starts at head.
   • fast pointer starts at head.next (or head, but head.next is often used to ensure fast is ahead initially).

2. Traverse the List: We iterate using a while loop as long as fast and fast.next are not None. This ensures we don't run into an error if the list ends.

   • In each step, slow moves one step (slow = slow.next).
   • fast moves two steps (fast = fast.next.next).

3. Cycle Detection:

   • If at any point slow and fast pointers meet (i.e., slow == fast), it means there is a cycle in the linked list, and we return True.

4. No Cycle: If the loop finishes (meaning fast or fast.next became None), it implies that fast reached the end of the list without meeting slow. This indicates there is no cycle, and we return False.

Time and Space Complexity:

• Time Complexity: O(N), where N is the number of nodes in the linked list. In the worst case (no cycle or cycle at the very end), the fast pointer traverses the entire list. If there is a cycle, the fast pointer will eventually catch the slow pointer within the cycle.
• Space Complexity: O(1), as we only use a few extra pointers.