56. Invert Binary Tree

Problem Statement

Given the root of a binary tree, invert the tree, and return its root.

Example 1:

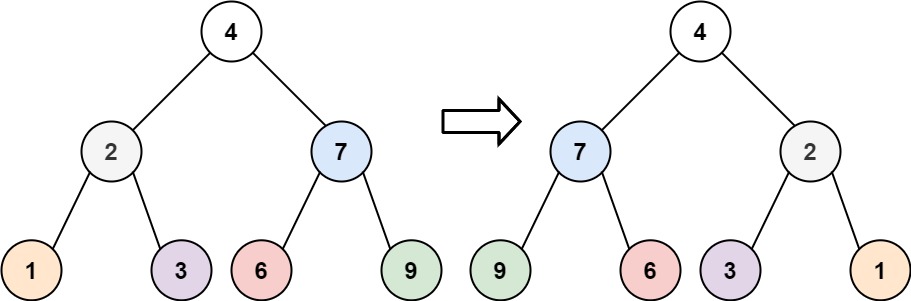
Input: root = [4,2,7,1,3,6,9] Output: [4,7,2,9,6,3,1]

Example 2:

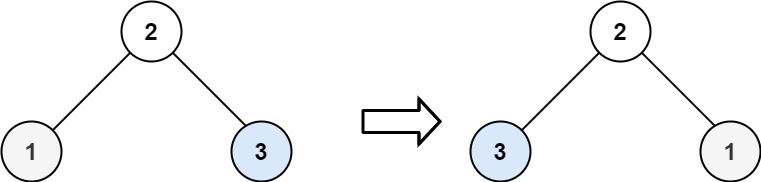
Input: root = [2,1,3] Output: [2,3,1]

Example 3:

Input: root = [] Output: []

Solution

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None

        # Swap the left and right children
        root.left, root.right = root.right, root.left

        # Recursively invert the left and right subtrees
        self.invertTree(root.left)
        self.invertTree(root.right)

        return root

Explanation

This problem can be solved elegantly using recursion.

Core Idea: To invert a binary tree, we need to swap the left and right children of every node in the tree.

Recursive Approach:

1. Base Case: If the root is None (an empty tree or a null child), there's nothing to invert, so we return None.

2. Recursive Step:

   • Swap Children: For the current root node, we swap its left and right children. Python's tuple assignment makes this very concise: root.left, root.right = root.right, root.left.
   • Recurse on Subtrees: After swapping the children of the current node, we recursively call invertTree on the (now new) root.left and root.right subtrees. This ensures that the inversion process is applied to all nodes down to the leaves.

3. Return Root: Finally, we return the root of the inverted tree.

Time and Space Complexity:

• Time Complexity: O(N), where N is the number of nodes in the binary tree. We visit each node exactly once.
• Space Complexity: O(H) in the worst case, where H is the height of the tree. This is due to the recursion stack. In a skewed tree, H can be N (O(N)), and in a balanced tree, H is log N (O(log N)).