27. Clone Graph
Problem Statement
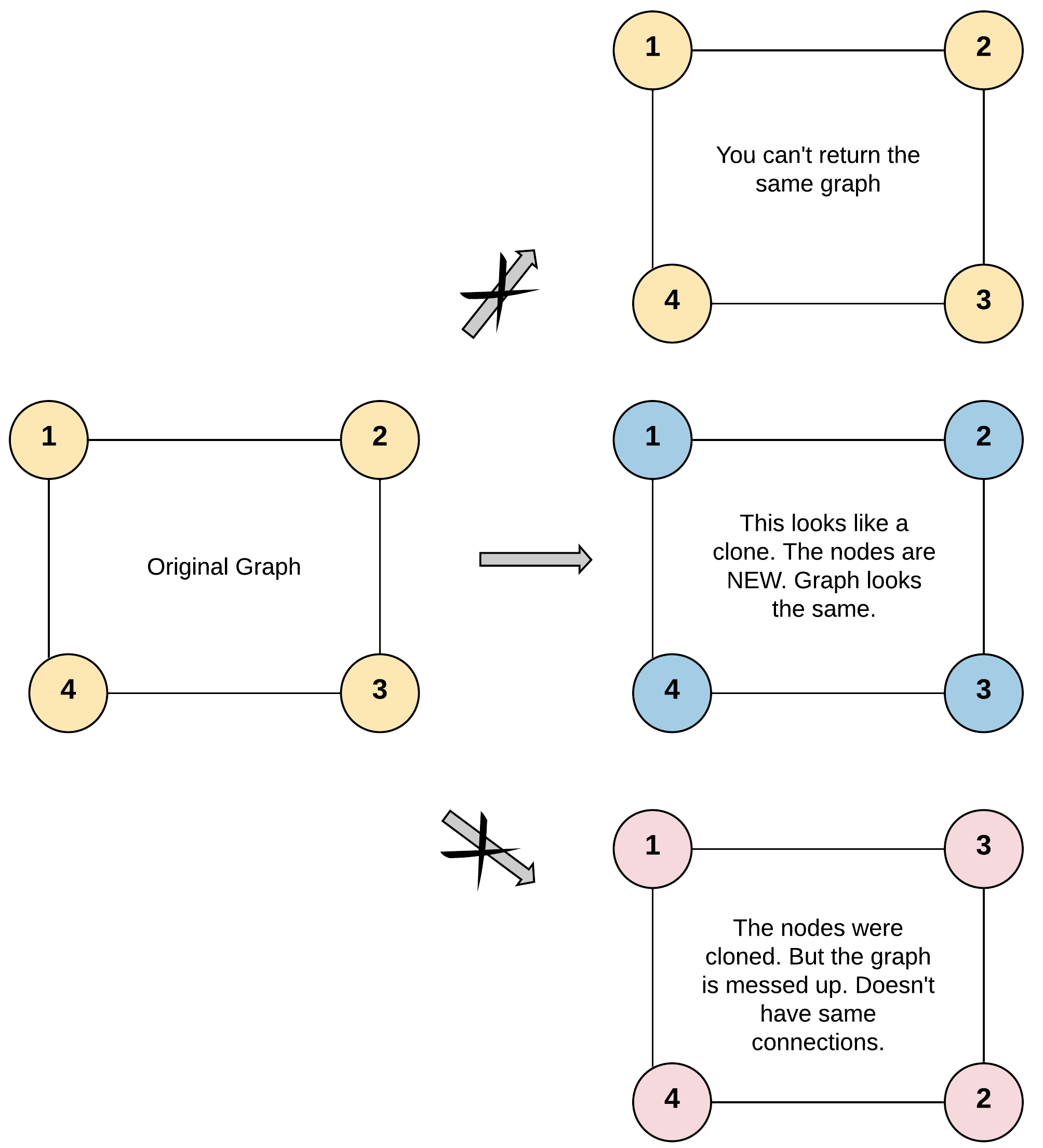
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
Test case format:
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
Input: adjList = [[2,4],[1,3],[2,4],[1,3]] Output: [[2,4],[1,3],[2,4],[1,3]] Explanation: The original graph and its clone have the same adjacency list.
Example 2:
Input: adjList = [[]] Output: [[]] Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = [] Output: [] Explanation: This represents an empty graph. There are no nodes in this graph.
Solution
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node:
return None
# A hash map to store the mapping from original nodes to their copies
old_to_new = {}
def dfs(original_node):
# If we have already cloned this node, return the clone
if original_node in old_to_new:
return old_to_new[original_node]
# Create a new node (the copy)
copy_node = Node(original_node.val)
old_to_new[original_node] = copy_node
# Recursively clone all the neighbors
for neighbor in original_node.neighbors:
copy_node.neighbors.append(dfs(neighbor))
return copy_node
return dfs(node)
Explanation
To create a deep copy of a graph, we need to traverse the entire graph and create a new copy for each node and each edge. A simple traversal (like DFS or BFS) is not enough, as we might get stuck in cycles or re-process nodes.
The key is to use a hash map (dictionary) to keep track of the nodes that have already been copied. This map, old_to_new, will store the mapping from an original node to its corresponding new, cloned node.
The algorithm works as follows (using Depth-First Search - DFS):
- Base Case: If the input
nodeisNone, we returnNone. old_to_newMap: This map is the core of the solution. Before cloning a node, we check if it's already in our map.- DFS Traversal:
- The
dfsfunction takes an original node as input. - Check the map: If the original node is already in
old_to_new, it means we've already created its copy. We simply return the copy from the map. This prevents infinite loops in graphs with cycles. - Create a copy: If the node is not in the map, we create a new
Nodewith the same value. - Update the map: We immediately add the mapping from the original node to our new copy in the
old_to_newmap. This is crucial to do before traversing its neighbors. - Clone neighbors: We then iterate through all the
neighborsof the original node. For each neighbor, we make a recursive call todfs. The return value of this call (which is the cloned neighbor) is appended to theneighborslist of ourcopy_node.
- The
- Return: The initial call to
dfs(node)starts the process, and it will eventually return the head of the new, cloned graph.
This approach ensures that each node is copied exactly once. The time complexity is O(N + E), where N is the number of nodes and E is the number of edges, as we visit each node and edge once. The space complexity is O(N) for the old_to_new map and the recursion stack.