62. Binary Tree Level Order Traversal

Problem Statement

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

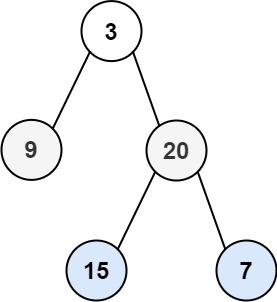
Binary Tree Level Order Traversal Example 1

Input: root = [3,9,20,null,null,15,7] Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1] Output: [[1]]

Example 3:

Input: root = [] Output: []

Solution

from collections import deque

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def levelOrder(self, root: TreeNode) -> list[list[int]]:
        result = []
        if not root:
            return result

        queue = deque([root])

        while queue:
            level_size = len(queue)
            current_level_nodes = []
            for _ in range(level_size):
                node = queue.popleft()
                current_level_nodes.append(node.val)

                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            result.append(current_level_nodes)

        return result

Explanation

This problem is a classic application of Breadth-First Search (BFS).

Core Idea: BFS explores a tree level by level. We use a queue to keep track of the nodes to visit.

  1. Initialization:

    • Create an empty list result to store the level order traversal.
    • If the root is None, return an empty result.
    • Initialize a deque (double-ended queue) and add the root to it.

  2. Level-by-Level Traversal:

    • The while queue: loop continues as long as there are nodes to visit.
    • Inside the loop, we first get the level_size (the number of nodes currently in the queue). This is crucial because it tells us how many nodes belong to the current level.
    • Create an empty list current_level_nodes to store the values of nodes at the current level.
    • Iterate level_size times:
      • Dequeue a node from the front of the queue.
      • Append node.val to current_level_nodes.
      • If the node has a left child, enqueue it.
      • If the node has a right child, enqueue it.
    • After processing all nodes at the current level, append current_level_nodes to the result.

  3. Return Result: Once the queue is empty, all nodes have been visited, and result contains the level order traversal.

Time and Space Complexity:

  • Time Complexity: O(N), where N is the number of nodes in the binary tree. Each node is visited and processed exactly once.
  • Space Complexity: O(W) in the worst case, where W is the maximum width of the tree (the maximum number of nodes at any single level). In a complete binary tree, W can be N/2, so O(N). In a skewed tree, W is 1, so O(1).