58. Balanced Binary Tree

Problem Statement

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

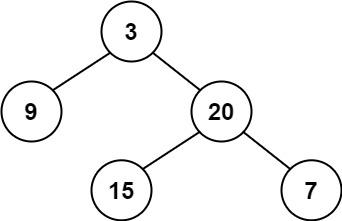
Input: root = [3,9,20,null,null,15,7] Output: true

Example 2:

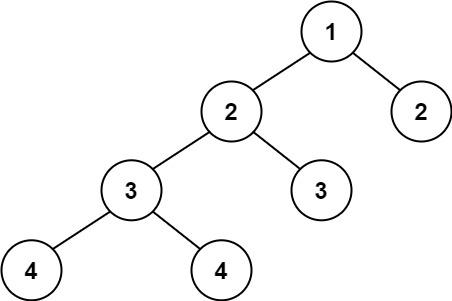
Input: root = [1,2,2,3,3,null,null,4,4] Output: false

Example 3:

Input: root = [] Output: true

Solution

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def dfs_height_check(node):
            if not node:
                return 0  # Height of an empty tree is 0

            left_height = dfs_height_check(node.left)
            if left_height == -1:  # Left subtree is unbalanced
                return -1

            right_height = dfs_height_check(node.right)
            if right_height == -1:  # Right subtree is unbalanced
                return -1

            # Check if current node is balanced
            if abs(left_height - right_height) > 1:
                return -1

            # Return the height of the current subtree
            return 1 + max(left_height, right_height)

        return dfs_height_check(root) != -1

Explanation

This problem can be solved efficiently using a recursive Depth-First Search (DFS) approach. The key is to check the balance condition while simultaneously calculating the height of each subtree.

Core Idea: We need to check two things for each node:

1. Its left subtree is balanced.
2. Its right subtree is balanced.
3. The absolute difference between the heights of its left and right subtrees is no more than 1.

Recursive dfs_height_check Function:

• This function returns the height of the subtree rooted at node if it's balanced, and -1 if it's unbalanced.

• Base Case: If node is None, its height is 0, and it's considered balanced. Return 0.

• Recursive Calls:

  • Recursively call dfs_height_check on the node.left to get left_height.
  • Recursively call dfs_height_check on the node.right to get right_height.

• Check for Unbalanced Subtree: If left_height or right_height is -1, it means one of the subtrees is already unbalanced. In this case, the entire tree rooted at node is also unbalanced, so we propagate the -1 up.

• Check Current Node's Balance: If both subtrees are balanced, we then check if the current node itself is balanced by comparing abs(left_height - right_height). If the difference is greater than 1, return -1.

• Return Height: If all checks pass, the current subtree is balanced, and its height is 1 + max(left_height, right_height).

Main Function: The isBalanced function simply calls dfs_height_check on the root and returns True if the result is not -1, indicating a balanced tree.

Time and Space Complexity:

• Time Complexity: O(N), where N is the number of nodes in the binary tree. Each node is visited exactly once.
• Space Complexity: O(H) in the worst case, where H is the height of the tree, due to the recursion stack. In a skewed tree, H can be N (O(N)), and in a balanced tree, H is log N (O(log N)).